17 June 2020
A graph is simply a collection of:
- Vertices or nodes
- Edges between vertices
For example, the graph in the image below has 6 vertices (labelled 1 to 6), and 7 edges.

Graphs are also sometimes called networks. We usually use “network” for very large graphs with many vertices (e.g. a social network, or a transport network), but there’s no fixed rule on when to use “graph” and when to use “network”. Both are fine.
Graphs and Matrices
At first sight, it may seem like graphs have nothing to do with matrices: graphs are like drawings, while matrices are tables of numbers.
But in fact, any graph has an adjacency matrix that completely defines the graph.
The adjacency matrix $A$ of a graph $G$ is an $n \times n$ matrix where:
- $n$ is the number of vertices in $G$ (assume that the vertices are labelled 1,2,… $n$)
- $A_{ij} = 1$ if there is an edge between vertex $i$ and $j$
- $A_{ij} = 0$ if there is no edge between vertix $i$ and $j$
So the adjacency matrix tells us which vertices are adjacent to each other.
The adjacency matrix of the graph above is given by:
\[\left(\begin{matrix}0 & 1 & 0 & 0 & 1 & 0\\1 & 0 & 1 & 0 & 1 & 0\\0 & 1 & 0 & 1 & 0 & 0\\0 & 0 & 1 & 0 & 1 & 1\\1 & 1 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0\end{matrix}\right)\]You can check this by going through the matrix row by row. Row $i$ tells you which other vertices you can reach from vertex $i$, by following an edge.
Directed and undirected graphs
You may have noticed that the matrix above is symmetric. This is because the graph above is an undirected graph, which just means that the edges have no “direction”. For example, since $4$ and $6$ are connected by an edge, both $A_{46}$ and $A_{64}$ are set to $1$.
A directed graph is a collection of:
- Vertices or nodes
- Directed edges or arrows between vertices
Here’s an example of a directed graph that we saw in our first lecture, and its adjacency matrix:
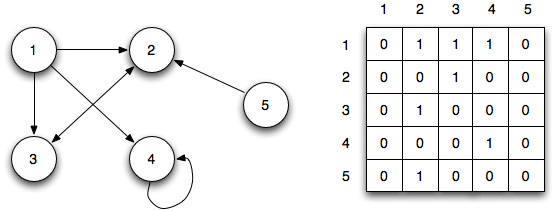
Row $i$ of the matrix tells you which other vertices you can get to from vertex $i$ by following an arrow.
Some things to note:
- The edges now have directions, indicated by the arrow head.
- The adjacency matrix is no longer symmetric.
Notice also that vertices 2 and 3 are connected by an arrow with two heads, so the $(2,3)$ and $(3,2)$ entries of the adjacency matrix are both $1$. This is similar to having an undirected edge between them in an undirected graph.
In fact, undirected graphs are special cases of directed graphs, where every edge is treated as an “arrow with two heads”.
You can think of an undirected graph as a network of two-way roads, while a directed graph is a network of one-way roads with the arrows indicating the direction.

Homework
Question 1
Here are some situations that can be represented with graphs.
- Friend network
- Family network
- Webpages and links between them
- Road network
Come up with a situation that can be represented with graphs, that is not in the above list.
Question 2
Choose two of the situations from Question 1 (you can choose the situation you came up with). For each situation, answer the following questions:
- What are the vertices of the graph?
- Is it directed or undirected?
- When is there an edge from one vertex to another?
There may not be one right answer for these questions. It all depends on how you want to represent the situation.
Question 3
For the situations that you chose in Question 2, draw a simple example of a graph that represents it, and its corresponding adjacency matrix. (An example will do: You don’t have to draw your whole friend network, or include real names!)
Bonus Question
This is just something for you to think about. Suppose you want to use a graph to represent JC students and the subjects they are taking. How would you do it with graphs? (If you did come up with a graph, you can use this for Questions 1,2,3 if you want.)
Discussion Question
This is for discussion during our next Zoom meeting: What situation would you be interested in representing with graphs? This does not need to be any of the above situations. You can also think about what situations you might want to study for SSEF.