1. Random walks on graphs

In this project, we will investigate the theory behind random walks on graphs, and see how these methods are applied to real-world problems.

In a random walk on a graph, we start on any node of the graph, then walk along any of its edges with equal probability. This brings us to another node, and we repeat the process again. After many iterations, we can compute the probability that we will end up at any particular node.

For example, consider the following graph:

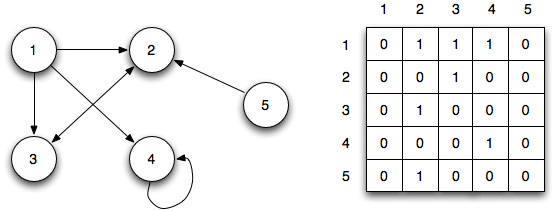
Node 1 is connected to nodes 2,3 and 4. So if we start at node 1, there is a $1/3$ probability that we will end up at node 2, and similarly for nodes 3 and 4. At the next step, we start at nodes 2,3 and 4 and repeat the process. If we keep doing this, what node will we end up at? We can’t be sure that we’ll definitely be on any particular node, but we can compute the probability that we end up there.

For the theory part of this project, we will:

• Learn how to couch random walks as matrix multiplications
• Understand how this is related to eigenvalues and eigenvectors
• Show that a random walk always converges to an equilibrium distribution
• Understand what a Markov process is, and how this is a special case of a Markov process

For applications, we will apply this to:

• Transport networks
• Network of hyperlinked webpages

For transport networks, we see how a “random traveller” model helps to identify central nodes in the network. For networks of webpages, we will see how Google’s PageRank algorithm uses a “random surfer” model to identify relevant webpages.

2. Recommendation Systems

In this project, we will investigate the use of linear algebra and graph theory in recommendation systems.

Suppose we have a large database of users and movies: we know which users have watched which movies, as well as the user’s rating (on a scale of 1 to 5 stars) for the movies they have watched.

The goal of a recommendation system is this: based on our knowledge of past movies a user $x$ has watched and rated, can we:

• Predict $x$’s ratings for movies that $x$ has not watched (the “?” in the picture above)
• Use this to recommend movies that $x$ will like

To do this, we find other users that have similar tastes to $x$, and use their ratings on other movies to estimate $x$’s ratings on those movies. But what does “similar tastes” mean, and how can we quantify it? We will see how to use linear algebra to answer this question.

For the theory part of this project we will:

• Learn how to represent our user-item database as a bipartite graph
• Understand how inner products give us a notion of “similarity”
• Learn about the singular value decomposition, which is a variant of the eigenvalue decomposition for non-square matrices

For applications, there are many public datasets with user-item ratings that we can apply this to:

• Movies (Movielens, IMDB)
• Music (Echo)
• Books (e.g. Goodreads)
• TV shows (e.g. Netflix)

We can choose a particular area to focus on (e.g. just books, or just movies), and try to:

• Identify clusters of similar users, and similar items (e.g. for movies, can the data help us cluster movies into Action, Horror, Comedy etc.?)
• Build a simple recommendation system that, given a list of movies that you like, recommends other movies to you