Partitions and Posets
In this post, we generate the Hasse diagram of a set partition.
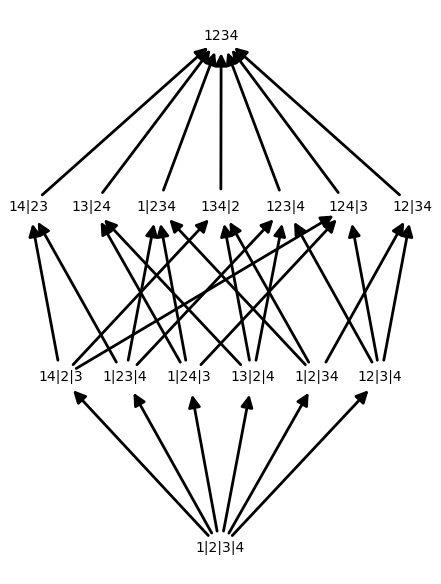
The following piece of code generates the image above.
Read on for an explanation of the code.
Partitions
A partition of a set $X$ is a collection $p$ of non-empty subsets of $X$ such that $X$ is the disjoint union of these sets.
In SAGE, you can get the set of all partitions of the $N$ element set {$1,2,\dots,N$} using SetPartitions:
Refinements
Each item in the preceding list is a partition of $X$. The elements of each partition are called blocks. At the top of the list, we see the trivial partition consisting of just one block, $X$. At the other end, we see the singleton partition consisting of $|X|$ blocks, where each block contains a single element of $X$. All other partitions of $X$ fall somewhere in-between these two partitions.
We can make this notion of “in-betweenness” precise by defining a relation on the partitions of $X$. We say that $q$ is a refinement of $p$ if each block of $q$ is contained in some block of $p$.
In Sage, you can see the refinements of a partition using the method refinements():
Posets
For a fixed $X$, the set $\mathcal{P}$ of all partitions of $X$ has the structure of a poset given by $q \leq p$ if $q$ is a refinement of $p$.
In Sage, we can construct a Poset by specifying an underlying set $P$ along with a function $f:P\times P \to$ {$\text{True},\text{False}$} where
The resulting poset can be visualized via its Hasse diagram, which is a directed graph with paths from $q \to p$ if $q \leq p$. We can generate a Hasse diagram of a poset using the show() method.
The final piece of code (at the top of the page) combines everything above to produce the Hasse diagram of a set. The function Partition_Poset first generates the set of partitions of an $N$ element set, then converts it to a poset. The function p_label relabels the partitions so that they look prettier. I’ve also tweaked some options in the show() method to make things look nicer.