This post illustrates the Argument Principle.

Let $f$ be a polynomial, and $C$ be (an arc of) a circle of radius $R$ centered at the origin.

The code below generates 2 plots. The first plot shows the domain of $f$. We plot the roots of $f$ together with $C$. Let $n_1$ be the number of roots contained within $C$.

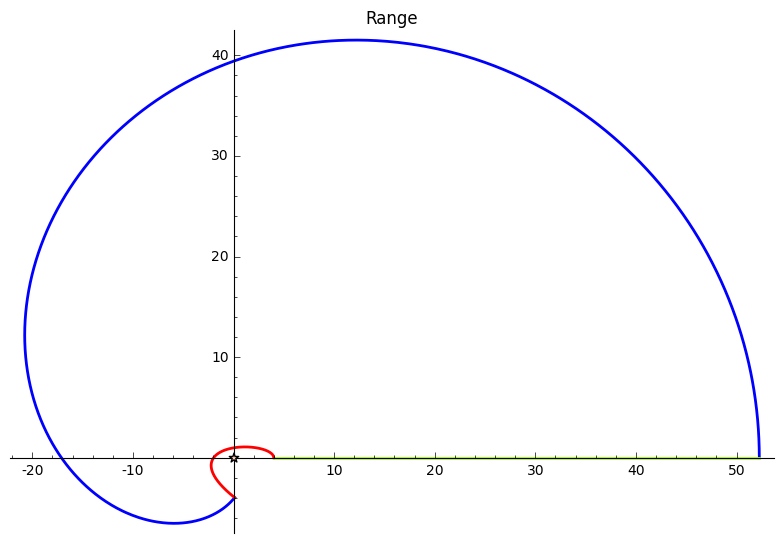
The second plot shows the range of $f$. We plot $f(C)$, along with a marker at the origin. Let $n_2$ be the number of times the curve winds around the origin.

You can verify that $n_1 = n_2$. As you vary the radius $R$, observe how $C$ and $f(C)$ change, and how this affects $n_1$ and $n_2$.