To sum up the subgroup lattice series, I’ve written a subgroup lattice generator. It’s powered by Sage and GAP, and allows you to view the lattice of subgroups or subgroup conjugacy classes of a group from your browser.

Normal subgroups are colored green. Additionally, the center is blue while the commutator subgroup is pink.

Showing the full subgroup lattice can get messy for large groups. If the option Conjugacy classes is selected, the viewer only shows the conjugacy classes of subgroups (i.e. all subgroups that are conjugate are combined into a single vertex).

The edge labels indicate how many subgroups of one conjugacy class a given representative subgroup of another conjugacy class contains, or how many subgroups of one conjugacy class a given representative subgroup of another conjugacy class is contained by. The labels are omitted if these numbers are 1. The edge colors indicate whether the subgroups in the “smaller” conjugacy class are normal subgroups of those in “larger” conjugacy class.

For instance, the group C15 : C4 (of order 60; the colon stands for semi-direct product and is usually written $\rtimes$) contains 5 subgroups isomorphic to C3 : C4, which in turn contains 3 subgroups isomorphic to C4 and 1 subgroup isomorphic to C6 (the 5 belows to another edge). The edge colors indicate that C6 is a normal subgroup of C3 : C3 whereas C4 is not. For further information on group descriptors, click here.

As mentioned in the previous post, labelling the edges requires taking apart the poset plotting code. I had to extract the Hasse diagram of a poset as a graph and modifying the edge labels directly. This explains why the code is much longer than in previous posts.

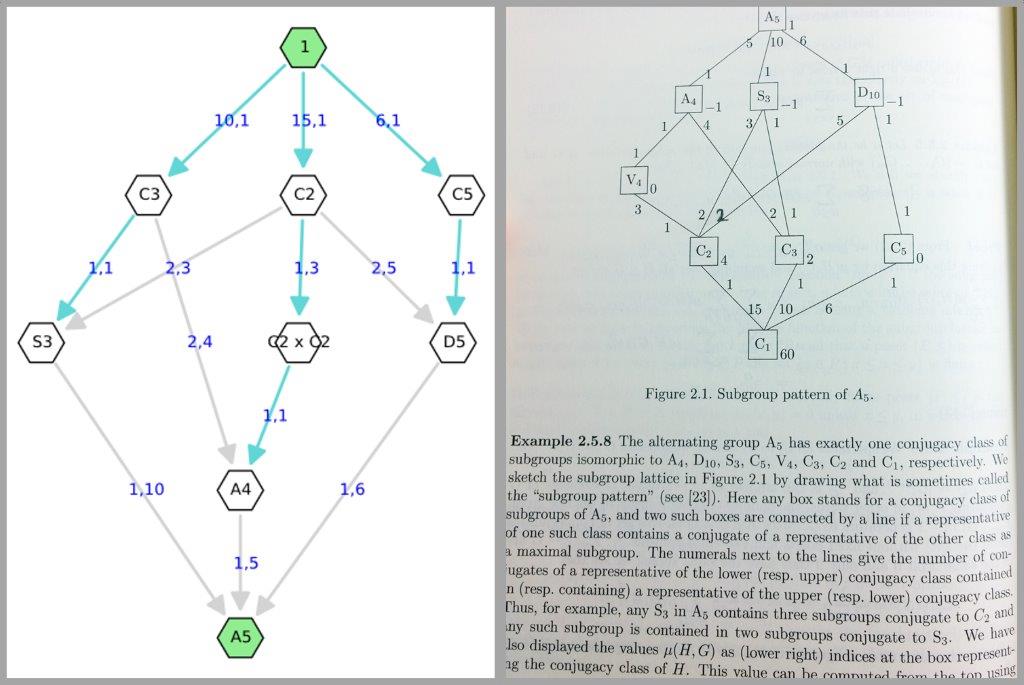
Finally, while verifying the results of this program, I found an error in this book! The correction has been pencilled in. The original number printed was 1.

This is the last post on subgroup lattices. My next post will be the start of a new series on doing represntation theory in Sage.